Probabilités
- Calcul d'une probabilité conditionnelle \(p_B (A)\)
- Construire un arbre pondéré en lien avec une situation réelle
- Déterminer des probabilités à l'aide d'un arbre pondéré
- Indépendance de deux évènements
IRappels
1Généralités
- L'événement \(A \cup B\) est constitué des issues qui appartiennent soit à A, soit à B, soit aux deux ensembles.
- L'événement \(A \cap B\) est constitué des issues qui appartiennent à la fois à A et à B.
- L'évènement \(\bar{A}\) est constitué des issues qui ne sont pas des issues de A
- \(A \cup B\) se lit « \(A\) union \(B\) » ou « \(A\) ou \(B\) »
- \(A \cap B\) se lit « \(A\) inter \(B\) » ou « \(A\) et \(B\) »
- \(\bar{A}\) se lit « \(A\) barre » ou « le contraire de \(A\) »
Dans l'expérience "tirer un dé à 6 faces", on note considère les évènement :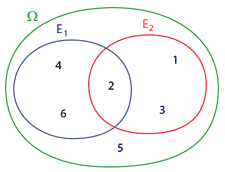 
Il est possible d'obtenir un des deux évènements, les deux à la fois ou aucun des deux :
- \(A\) "obtenir un nombre pair" : \(A = \{2,4,6\}\)
- \(B\) "obtenir moins que 4" \(B = \{1,2,3\}\)
Il est possible d'obtenir un des deux évènements, les deux à la fois ou aucun des deux : - \(A\cup B\) "obtenir un nombre pair ou un nombre plus petit que 4" : $$A\cup B = \{1,2,3,4,6\}$$
- \(A\cap B\) "obtenir à la fois un nombre pair et plus petit que 4" : $$A\cap B = \{2\}$$
- \(\bar{A}\) "obtenir un nombre impair" : $$\bar{A} = \{1,3,5\}$$
2Calculs
Deux évènement \(A\) et \(B\) sont incompatibles quand \(A\cap B = \emptyset\).
Concrètement, deux évènement incompatibles ne peuvent pas se produire en même temps.
Les évènement "faire un nombre pair" et "faire un nombre impair" sont incompatibles.
L'intersection entre \(\{2,4,6\}\) et \(\{1,3,5\}\) est vide : \(A\cap B = \emptyset\).
Soit \(A\) un évènement quelconque et \(\bar{A}\) sont évènement contraire. Alors : $$p (\bar{A}) = 1 - p (A)$$
On reprend les mêmes exemples :
- \(\bar{A}\) "otenir un nombre impair" a pour probabilité : \(p (\bar{A}) = 1 - p (A) = 1 - \frac{1}{2} = \frac{1}{2}\)
- \(\bar{B}\) "otenir un nombre plus grand que 3" a pour probabilité : \(p (\bar{B}) = 1 - p (B) = 1 - \frac{1}{2} = \frac{1}{2}\)
Pour tous évènements \(A\) et \(B\) (incompatibles ou pas) : $$p (A \cup B) = p (A) + p (B) - p (A \cap B)$$
On reprend le même exemple où \(A\) est "obtenir un nombre pair" et \(B\) est "faire moins que 4".
On a \(p (A) = \frac{1}{2}\), \(p (B) = \frac{1}{2}\) et comme \(A \cap B = \{2\}\) contient un seul élément \(p (A \cap B) = \frac{1}{6}\).
Si on applique la formule : $$p (A \cup B) = p (A) + p (B) - p (A \cap B) = \frac{3}{6} + \frac{3}{6} - \frac{1}{6} = \frac{5}{6}$$
Ici, on peut vérifier facilement que c'est vrai car \(A \cup B\) est l'évènement "obtenir n'importe quel nombre plus petit que 4 ou un nombre pair", c'est à dire \(\{1,2,3,4,6\}\) qui contient 5 issues.IIProbabilité conditionnelle
Dans cette partie, on note \(A\) et \(B\) deux évènements d'une expérience aléatoire.
Lorsque deux évènements \(A\) et \(B\) sont étudiés conjointement, il est possible de représenter les données numériques sous la forme d'un tableau à double entrées avec la répartition suivante : $$ \begin{array}{ |c|c|c|c|} \hline & \text{Evènement} B &\text{Evènement} \bar{B}&\text{total}\\ \hline \text{Evènement} A & A\cap B & A\cap \bar{B} & A \\ \hline \text{Evènement} \bar{A} & \bar{A}\cap B & \bar{A}\cap \bar{B} & \bar{A} \\ \hline \text{total} & B & \bar{B} & \text{effectif total de } \Omega\\ \hline \end{array} $$
On note \(p_A (B)\) la probabilité de \(B\) sachant que A s'est déjà produit.
Une probabilités conditionnelle \(p_A (B)\) est liée aux évènements \(A\), \(B\)et \(A \cap B\) par la formule suivante :
\(p (A \cap B) = p (A) p_A (B)\)
Il est donc possible de calculer la probabilité conditionnelle par la formule déduite :
\(p_A (B) = \frac{p (A \cap B)}{p (A)}\)
A l'épreuve du permis de conduire, on a observé les résultats dans le tableau ci-dessous sur un échantillon de 503 personnes se présentant pour la première fois. On utilise les notations suivantes :
En choisissant un élève au hasard, il y a une probabilité de \frac{11}{25} qu'il ne pratique aucun de ces sports.
- \(C\) : candidats ayant fait sa conduite accompagnée
- \(A\) : candidats admis à l'issue de l'épreuve
- \(\bar{C}\) : candidats n'ayant pas fait de conduite accompagnée
- \(\bar{A}\) : candidats refusés à l'issue de l'épreuve
- La probabilité \(p (A)\) qu'un élève soit admis vaut : $$p (A)=\frac{275}{500}=0,55$$
- La probabilité \(p (C)\) qu'un élève ait pratiqué la conduite accompagnée vaut : $$p (C)=\frac{89}{500}= 0,178$$
- La probabilité \(p (A \cup C)\) qu'un élève soit admis et ait pratiqué la conduite accompagnée vaut : $$ p (A \cap C)=\frac{75}{500}=0,15$$
- La probabilité \(p_C (A)\)qu'un élève soit admis sachant qu'il a pratiqué la conduite accompagnée vaut : $$ p_C (A)=\frac{75}{89}\simeq 0,84$$
IIIArbre pondéré
Les arbres mathématiques sont souvent utilisés pour représenter des scénarios à choix avec différentes issues possibles. Ils sont
donc utilisés en probabilité lorsque l'on étudie plusieurs évènements.
Sur un arbre pondéré, on représente les évènements possibles avec \(A\) antérieur à \(B\). Les probabilités conditionnelles se lisent sur les deuxièmes branches en partant du premier noeud :
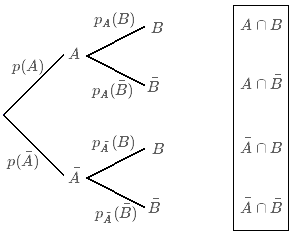
Deux propriétés se vérifient sur un arbre pondéré :
- La somme des probabilités de branches issues d'un même noeud, vaut 1 : $$ p (A) + p (\bar{A}) = 1$$ $$ p_A (B) + p_A (\bar{B})=1$$
- La probabilité d'un évènement correspondant à un chemin vaut le produit des probabilités de chaque branche du chemin : $$p (A) \times p_A (B) = p (A \cap B)$$ $$p (A) \times p_A (\bar{B}) = p (A \cap \bar{B})$$
Représentons à l'aide d'un arbre, une expérience aléatoire sur un lycée de 1000 élèves où nous tirons au hasard la fiche de renseignement d'un élève :
La situation se représente par un arbre pondéré :
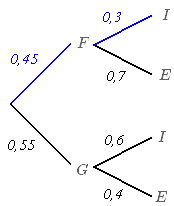
- L'univers \(\Omega\)est l'ensemble des élèves
- L'évènement \(G\) est "l'élèvé est un garçon", l'évènement contraire \(\bar{G}\), noté \(F\) est "l'élève est une fille"
- L'évènement \(E\) est "l'élèvé est externe", l'évènement contraire \(\bar{E}\), noté \(I\) est "l'élève est interne"
La situation se représente par un arbre pondéré :
Sur notre exemple, on peut lire les probabilités conditionnelles :
- La probabilité de choisir un élève interne parmi les filles est \(p_F (I)=0,3\)
- La probabilité de choisir un élève externe parmi les filles \(p_F (E)=0,7\)
- la probabilité de choisir un élève interne parmi les garçons \(p_G (I)=0,6\)
- la probabilité de choisir un élève externe parmi les garçons \(p_G (E)=0,4\)
- \(p (F) + p (G) = 1\)
- Le chemin bleu correspond à l'évènement \(F\cap I\) " l'élève est une fille interne", représente 30% de 45% des élèves, donc \(\frac{30}{100} \times \frac{45}{100} \times 100= 13,5%\) des élèves. On retrouve ce résultat en multipliant les probabilités des deux branches : \(0,45 \times 0,30 = 0,135\).
IVEvènements indépendants
Intuitivement, deux évènements sont indépendants si l'issus de l'un ne peux influer l'issue de l'autre.
On tire au hasard parmi 10 boules numérotées de \(0\) à \(9\) et indicernables au touché une boule, puis une deuxième. On appelle \(P_1\) l'évènement "tirer un nombre pair en premier" et \(P_2\) "tirer un nombre pair en second" :
- Si le tirage est sans remise, le fait de tirer une boule paire en premier influence grandement la possibilité de tirer un nombre pair en second. Les évènements \(P_1\) et \(P_2\) ne sont pas indépendants.
- Si le tirage est avec remise, chaque tirage se fera toujours parmi 10 boules numérotées de \(0\) à \(9\). Les deux évènements \(P_1\) et \(P_2\) sont donc indépendants.
Mathématiquement, on peut vérifier l'indépendance de deux évènements :
On dira que deux évènements sont indépendants si : $$ p (A\cap B) = p (A) p (B) $$
Intuitivement l'indépendance se comprend aussi par le fait que la probabilité \(p (A)\) est inchangée si \(B\) s'est produit avant (probabilité conditionnelle \(p_B (A)\)) :
On peut aussi dire que deux évènements \(A\) et \(B\) sont indépendants si \(p_B (A) = p (A)\).
On peut se demander si, à pile ou face, on a plus de chance d'obtenir deux fois de suite le même résultat (évènement \(B\)), si on a d'abord obtenu pile évènement \(A\).
- En jouant deux fois de suite à pile ou face, il y a \(4\) issues possibles : \(\{pp, pf, fp, ff\}\)
- La probabilité de faire deux fois le même résultat vaut donc \(p (B) = \frac{2}{4} = \frac{1}{2}\)
- La probabilité de commencer par pile \(p (A) = \frac{2}{4} = \frac{1}{2}\)
- La probabilité de commencer par pile et de faire deux fois le même résultat \(p (A\cap B) = \frac{1}{4}\)
- On vérifie bien que \(p (A) p (B) = \frac{1}{2}\times \frac{1}{2} = \frac{1}{4} = p (A\cap B) \)